2025年成考高起点《数学(理)》每日一练试题07月19日

2025年成考高起点《数学(理)》每日一练试题07月19日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、函数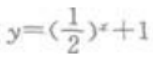的值域是（）。

• A：(0，＋∞)
• B：(－∞，＋∞)
• C：(1，＋∞)
• D：[1，＋∞)

答 案：C

解 析：

2、设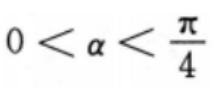，则 （）。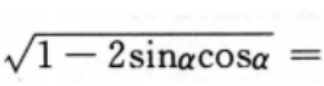

• A：sina+cosa
• B：—sing—cosa
• C：sing—coso
• D：cosa—sina

答 案：D

解 析：本题主要考查的知识点为三角函数的运算.当时，

3、从点M(x,3)向圆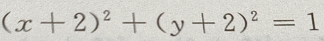作切线，切线的最小值等于（）  

• A：4
• B：
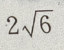
• C：5
• D：

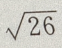
答 案：B

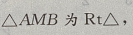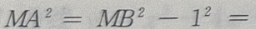
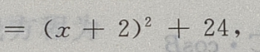
解 析：如图,相切是直线与圆的位置关系中的一种，此题利用圆心坐标、半径，求出切线长. 由圆的方程知,圆心为B(-2,-2),半径为1，设切点为A， 由勾股定理得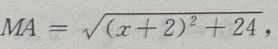， 当x+2=0时，MA取最小值，最小值为  

4、在△ABC中，∠C=90°，∠B=30°，D是BC上的一点，∠ADB=135°，AC=2，则BD等于（）。  

• A：
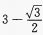
• B：
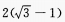
• C：
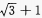
• D：

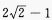
答 案：B

解 析：由已知得，AC=CD=2，设BD=x，在Rt△ABC中，BC=2cot30°=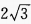  

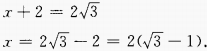
主观题

1、已知A（1，4），B（3，8），C（4，10）。求证A、B、C三点共线。  

答 案：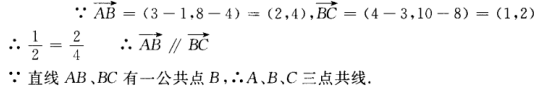

2、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得AB=120m,求河的宽

答 案：如图， ∵∠C=180°-30°-75°=75° ∴△ABC为等腰三角形，则AC=AB=120m 过C做CD⊥AB,则由Rt△ACD可求得CD==60m， 即河宽为60m  

3、已知x+x^-1=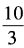，求x²+x-2的值。

答 案：由已知，得

4、在△ABC中如果sinA=2sinBcosC，求证：△ABC是等腰三角形。  

答 案：∴△ABC为等腰三角形。

填空题

1、椭圆的中心在原点，一个顶点和一个焦点分别是直线x+3y-6与两坐标轴的交点,则此椭圆的标准方程为（）  

答 案：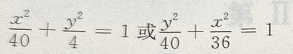

解 析：原直线方程可化为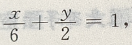交点(6,0),(0,2). 当点(6,0)是椭圆一个焦点,点(0,2) 是椭圆一个顶点时,c=6,b=2,当点(0,2) 是椭圆一个焦点,(6,0) 是椭圆一个顶点时,c=2,b-6,

2、已知A（0,1），B（1，2），存在一点P是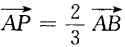，则点P的坐标是______。

答 案：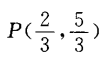

解 析：