2025年成考高起点《数学(理)》每日一练试题05月24日

2025年成考高起点《数学(理)》每日一练试题05月24日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、（2-3i）²=（）

• A：13-6i
• B：13-12i
• C：-5-6i
• D：-5-12i

答 案：D

解 析：

2、在△ABC中，若lgsinA-lgsinB-lgcos=lg2，则△ABC是（）

• A：以A为直角的三角形
• B：b=c的等腰三角形
• C：等边三角形
• D：钝角三角形

答 案：B

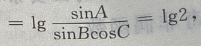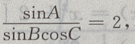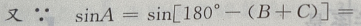
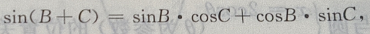
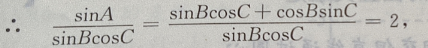
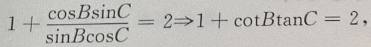
解 析：判断三角形的形状，条件是用一个对数等式给出先将对数式利用对数的运算法则整理。 ∵lgsinA-lgsinB-lgcos=lg2，由对数运算法则可得,左 两个对数底数相等则真数相等：即2sinBcosC=sinA 在△ABC中，∵A+B+C=180°，∴A=180°-（B+C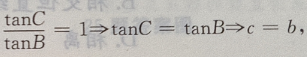）, 故为等腰三角形

3、设集合M={x||x-2|＜1}，N={x|x＞2}，则M∩N=（）

• A：{x|1＜x＜3}
• B：{x|x＞2}
• C：{x|2＜x＜3}
• D：{x|1＜x＜2}

答 案：C

解 析：M={x||x-2|＜1}解得{x|-1＜x-2＜1}={x|1＜x＜3}，故M∩N={x|2＜x＜3}

4、直线3x-4y-9=0与圆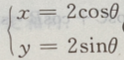(θ为参数)的位置关系是

• A：相交但直线不过圆心
• B：相交但直线通过圆心
• C：相切
• D：相离

答 案：A

解 析：方法一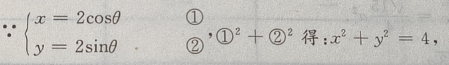： 圆心O（0,0），r=2，则圆心O到直线的距离为 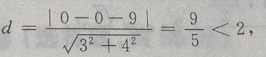0

主观题

1、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得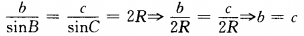

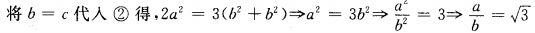
∴a：b=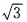：1
于是a：b：c=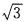：1：1。  

2、设函数f(x)= (Ⅰ)求f(x)的单调区间; (Ⅱ)求 f(x)的极值

答 案：(Ⅰ)函数的定义域为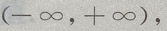 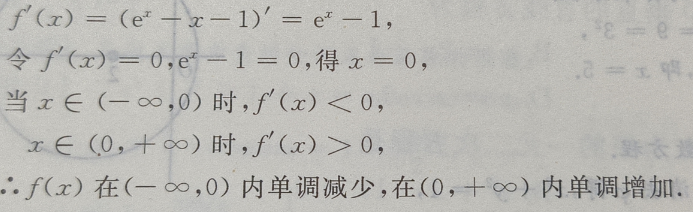(Ⅱ)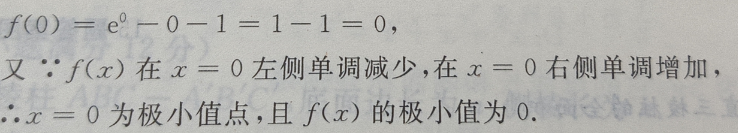  

3、空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  

答 案：根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式所以共可确定四个平面。

解 析：空间有n个点，如果其中任何三点不在同一直线上，可以确定个平面。  

4、计算 （1）tan5°+ cot5°- 2sec80°
（2）tan15°+cot15
（3）sin15°sin75°

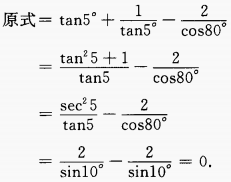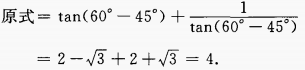答 案：（1）化切割为弦进行运算。 （2） （3）

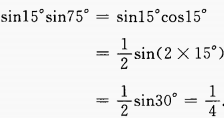
填空题

1、函数y=-x²+ax图像的对称轴为x=2，则a=______。  

答 案：4

解 析：本题主要考查的知识点为二次函数的性质 由题意，该函数图像的对称轴为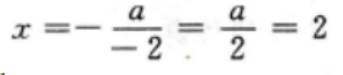

2、从甲、乙、丙3名学生中随机选2人，则甲被选中的概率为          .

答 案：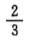

解 析：