2025年成考高起点《数学(理)》每日一练试题03月15日

2025年成考高起点《数学(理)》每日一练试题03月15日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

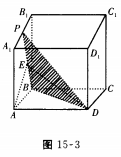
1、若P为正方体A1C中A1B1棱上的中点，则过P、B、D三点的平面与AA1B1B面所成的二面角的余弦值为（）。

• A：
• B：
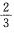
• C：
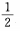
• D：

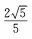
答 案：B

解 析：

2、在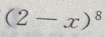的展开式中,的系数是

• A：448
• B：1140
• C：-1140
• D：-448

答 案：D

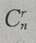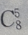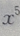解 析：直接套用二项式展开公式: 注:展开式中第r+1项的二项式系数与第r+1项的系数不同,此题不能只写出就为的系数  

3、(sinα+sinβ)²+(cosα+cosβ)²=（）。

• A：
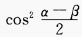
• B：
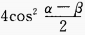
• C：
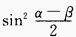
• D：

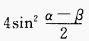
答 案：B

解 析：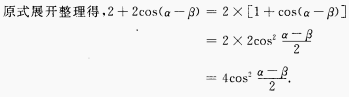

4、下列各式中，不成立的是（）。

• A：
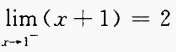
• B：
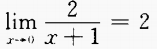
• C：
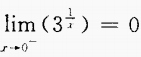
• D：

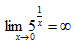
答 案：D

解 析：可用排除法，A、B、C均成立。

主观题

1、空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  

答 案：根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式所以共可确定四个平面。

解 析：空间有n个点，如果其中任何三点不在同一直线上，可以确定个平面。  

2、函数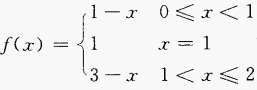在其定义域上是否连续？作出f（x）的图形。

答 案：f（x）的定义域为[0，2] 当0≤x<1时f（x）=1-x是连续的 当1 f(x)除了在x=1处不连续,在其定义域内处处连续,如图7-7.

3、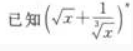 展开式的二项式系数之和比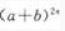展开式的二项式系数之和小240。 求：（1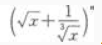）展开式的第3项；
（2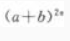）展开式的中间项。

答 案：

4、当自变量为何值时，函数y=2x³-3x²-12x+21有极值，其极值为多少？  

答 案：y'=6x²-6x-12=6（x-2）（x+1） 当x<-1或x>2时，y>0，当-1 故当x=-1时有极大值，其值为f（-1）=28 当x=2时有极小值，其值为f（2）=1

填空题

1、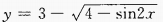的值域是______。  

答 案：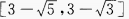

解 析：当sin2x=-1时，y最小值当 sin2x=1时,  

2、若tanα-cotα=1，则=______。

答 案：4

解 析：由立方差公式得,tan³α-cot³α=(tana-cotα)(tan²α+tanαcota+cot²α)(tana-cotα)[(tanα-cotα)²+3tanαcotα]=4