2025年成考高起点《数学(文史)》每日一练试题07月28日

2025年成考高起点《数学(文史)》每日一练试题07月28日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、下列函数在定义域内，既是奇函数又是增函数的是（）。

• A：y=sinx
• B：y=log2^x 
• C：y=x+8
• D：y=x³ 

答 案：D

2、已知向量a=（3,1），b=（-2,5），则3a-2b=（）。

• A：（2,7）
• B：（13，-7）
• C：（2，-7）
• D：（13，,13）

答 案：B

解 析：根据a=(3,1),b=(-2,5),则3a-2b=3×(3,1)-2×(-2,5)=(13,-7)  

3、过点A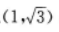与圆x²+y²=1相切的直线方程是（）

• A：
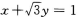
• B：
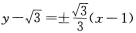
• C：
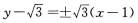
• D：以上都不是

答 案：D

解 析：【考点指要】本题主要考查的内容是利用点到直线的距离公式求直线的斜率，从而写出所求的直线方程，这是考试大纲要求掌握的概念．从近几年的试题分析可知，这类题的深度在今后成人高考中有可能加大，希望考生予以足够的重视．

4、在自然数1、2、…、100中任取一个数能被3整除的概率是（）。

• A：
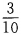
• B：
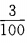
• C：
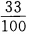
• D：

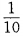
答 案：C

解 析：此题属于等可能事件的概率，n=100，m=33，其概率为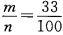，故应选C。  

主观题

1、若tanα、tanβ是关于x的方程mx²-(2m-3)x+m-2=0的两个实根，求tan(α+β)的取值范围

答 案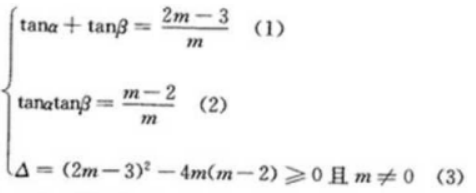： 由(1)(2)得，tan(a+β)=m-3/2;由(3)得m≤9/4且m≠0所以tan(a+β)的取值范围是(-∞，-3/2)U(-3/2，3/4)  

2、求（1+tan10°）（1+tan35°）的值。

答 案：原式=1+tan10°+tan35°+tan10°·tan35°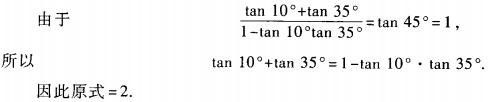

3、在△ABC中，已知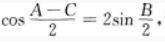证明a，b，c成等差数列。

答 案： 考点 本题主要考查三角函数的恒等变换以及积化和差公式的应用，积化和差有一定难度，请考生注意．

4、已知三角形的三边边长组成公差为1的等差数列，且最大角是最小角的二倍，求三边之长。  

答 案：三角形的三边边长分别为4，5，6。

填空题

1、一个问题在1小时内，甲能独立解决的概率是0.5，乙能独立解决的概率是0.4，两人在1小时内解决问题的概率是______。

答 案：0.7  

2、log₂[log₂（log₃81）]=______。  

答 案：1

解 析：由于log₃81=log₃3⁴=4，于是 原式=log₂（log₂4）=log₂2=1。