2025年成考专升本《高等数学二》每日一练试题10月16日
2025-10-16 11:28:52 来源:勒克斯教育网
2025年成考专升本《高等数学二》每日一练试题10月16日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析:
单选题
1、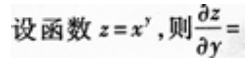 ()。
()。
- A:xy
- B:xylny
- C:xylnx
- D:yxy-1
答 案:C
2、已知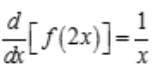 ,则
,则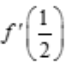 =().
=().
- A:
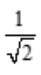
- B:
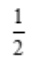
- C:2
- D:4
答 案:C
解 析:因为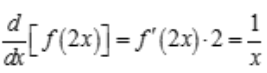 ,所以
,所以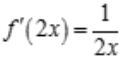 ,则
,则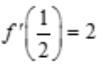 .
.
主观题
1、设生产某种产品的数量z与所用两种原料A的数量x吨和B的数量y吨间有关系式z=z(x,y)=xy,欲用100万元购买原料,已知A,B原料的单价分别为每吨1万元和每吨2万元,问购进两种原料各多少时,可使生产的产品数量最多?
答 案:解:当购进A原料x吨时,需花费x万元,此时,还可购进B原料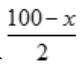 吨,函数z=xy变为关于x的一元函数,
吨,函数z=xy变为关于x的一元函数, ,其定义域为[0,100].求出z'=-x+50,令z'=0,即-x+50=0,解得x=50.当x<50时,z'>0;当x>50时,z'<0.所以x=50是函数
,其定义域为[0,100].求出z'=-x+50,令z'=0,即-x+50=0,解得x=50.当x<50时,z'>0;当x>50时,z'<0.所以x=50是函数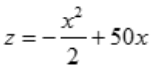 的极大值点,显然也是最大值点.
的极大值点,显然也是最大值点.
此时,y=25,即当购进A原料50吨.B原料25吨时,生产的产品数量最多.
2、证明:当x>1时,x>1+lnx.
答 案:证:设f(x)=x-1-lnx,则f'(x)= .当x>1时,f'(x)>0,则f(x)单调上升.所以当x>1时,f(x)>f(1)=0,即x-1-lnx>0,得x>1+lnx.
.当x>1时,f'(x)>0,则f(x)单调上升.所以当x>1时,f(x)>f(1)=0,即x-1-lnx>0,得x>1+lnx.
填空题
1、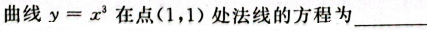
答 案: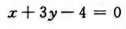
解 析: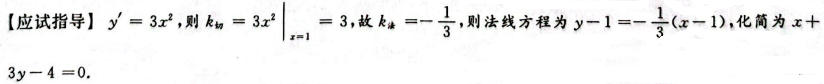
2、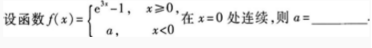
答 案:0
简答题
1、设D为曲线y=1-x2,直线y=x+1及x轴所围成的平面区域(如图1-3-1所示)。①求平面图形的面积;
②求平面图形D绕x轴旋转一周所成旋转体的体积Vx。
答 案: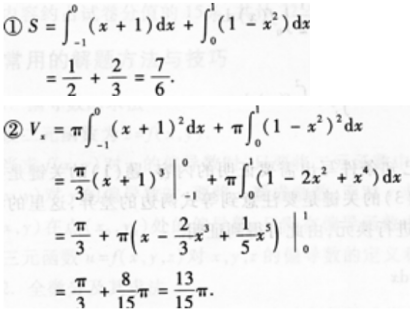
2、已知函数f(x)=ax3-bx2+cx在区间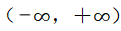 内是奇函数,且当x=1时,f(x)有极小值
内是奇函数,且当x=1时,f(x)有极小值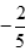 ,求另一个极值及此曲线的拐点.
,求另一个极值及此曲线的拐点.
答 案:f(x)=ax3-bx2+cx,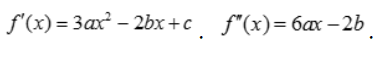 由于f(x)是奇函数,则必有x2的系数为0,即b=0.
由于f(x)是奇函数,则必有x2的系数为0,即b=0.
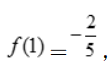 即a+c=
即a+c=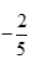 ,
,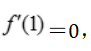 得3a+c=0.解得a=
得3a+c=0.解得a=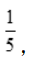 c=
c= 此时
此时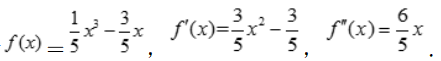 令
令 得
得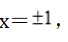
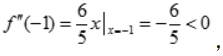 所以
所以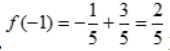 为极大值,
为极大值,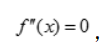 得x=0,x<0时,
得x=0,x<0时,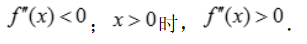 所以(0,0)为曲线的拐点.
所以(0,0)为曲线的拐点.



