2022年成考专升本《高等数学二》每日一练试题12月13日

2022年成考专升本《高等数学二》每日一练试题12月13日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、根据f(x)的导函数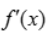的图像（如图所示），判断下列结论正确的是（ ）．

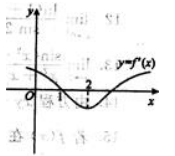
• A：在（∞，1）上f(x)是单调递减的
• B：在（∞，2）上f(x)是单调递减的
• C：f(1)为极大值
• D：f(1)为极小值

答 案：C

解 析：在x轴上方的曲线是表示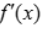>0,而x轴下方的曲线则表示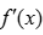<0,注在x＝1处的左边即x<1时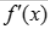>0,而2>x>1时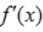<0，根据极值的第一充分条件可知f(1)为极大值．  

2、（）.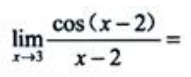

• A：1
• B：cos1
• C：0
• D：

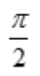
答 案：B

解 析：因为函数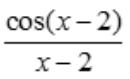在x=3处连续，故.

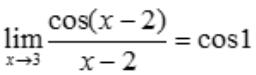3、下列说法正确的是（ ）．  

• A：如果x₀是函数y＝f(x)的极值点，则必有
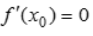
• B：如果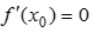，则x₀是函数y＝f（x）的极值点
• C：如果x₀不是函数y＝f(x)的极值点，且函数在x₀点可导，则必有
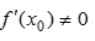
• D：如果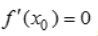.则x₀一定不是函数y＝f(x)的极值点

答 案：C

解 析：A项，如x=0是y=|x|的极值点，但不存在；B项，如y=x^3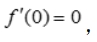，但x＝0不是极值点；D项，如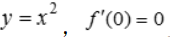且x＝0是极值点．

主观题

1、求函数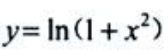的单调区间、极值、凹凸区间和拐点．

答 案：解：函数定义域为x∈R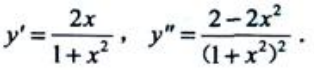，令y'＝0得ｘ＝0，令y"＝0得ｘ＝±1．函数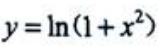的单调增加区间为（0，＋∞），单调减少区间为（∞，0）；y(0)＝0为极小值，无极大值．
函数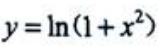的凸区间为（-∞，-1）∪（1，＋∞），凹区间为（-1，1），拐点为（-1，ln2）与（1，ln2）．

2、已知离散型随机变量X的概率分布为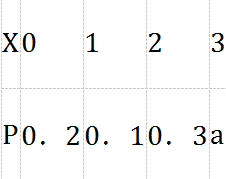（1）求常数a；
（2）求X的数学期望EX和方差DX．

答 案：解：（1）因为0.2＋0.1＋0.3＋a＝1，所以a＝0.4；（2）EX＝0×0.2＋1×0.1＋2×0.3＋3×0.4＝1.9；DX＝（0－1.9）²×0.2＋（1－1.9）²×0.1＋（2－1.9）²×0.3＋（3－1.9）²×0.4＝1.29．

3、计算．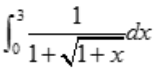

答 案：解：设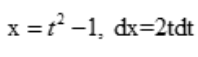，，当x＝0时，t＝1；x＝3时，t＝2．则原式可变换为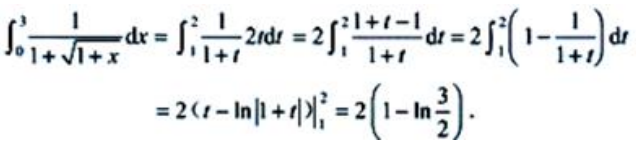

填空题

1、（）．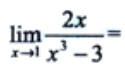

答 案：－1

解 析：．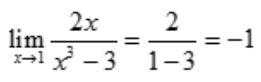

2、曲线y＝2x²＋3x－26上点M处的切线斜率是15，则点M的坐标是（）．

答 案：（3，1）

解 析：因为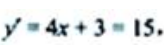解得x＝3，又y(3)＝2×3²＋3×3－26＝1，故点M的坐标是（3，1）．

3、函数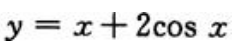在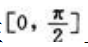上最大值为（）．

答 案：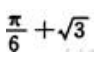

解 析：由得驻点为，，比较得y的最大值为

简答题

1、设函数求常数a。使f(x)在点x=0处连续。  

答 案： 要f(x)在点x=0处连续，则需所以a=1.