2025年成考专升本《高等数学一》每日一练试题07月12日

2025年成考专升本《高等数学一》每日一练试题07月12日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、设z=ysinx，则等于（）。  

• A：-cosx
• B：-ycosx
• C：cosx
• D：ycosx

答 案：C

解 析：本题考查的知识点为二阶偏导数。 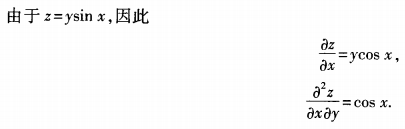可知应选C。  

2、设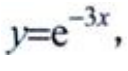则dy＝（）。

• A：
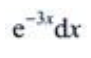
• B：
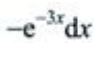
• C：
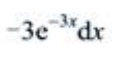
• D：

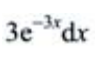
答 案：C

解 析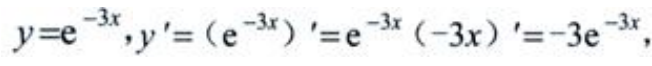：故．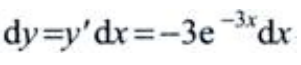

3、用待定系数法求微分方程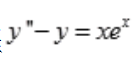的一个特解时，特解的形式是（）.（式中a、b是常数）

• A：
• B：
• C：
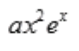
• D：

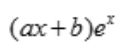
答 案：A

解 析：y″－y＝0的特征方程是r²－1＝0，特征根为r₁＝1，r₂＝－1.y″－y＝xe^x中自由项f（x）＝xe^x，a＝1是特征单根，则特解为y*＝x（ax＋b）e^x＝（ax²＋bx）e^x。

主观题

1、欲围造一个面积为15000平方米的运动场，其正面材料造价为每平方米600元，其余三面材料造价为每平方米300元，试问正面长为多少米才能使材料费最少?

答 案：解：设运动场正面围墙长为x米，则宽为，设四面围墙高相同，记为h，则四面围墙所用材料费用，f（x）为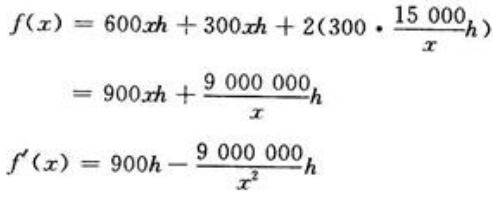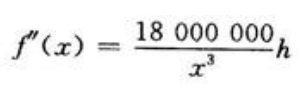令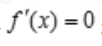得驻点x₁＝100，x₂＝－100（舍掉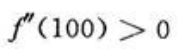），由于驻点唯一，且实际问题中存在最小值，可知x＝100米，侧面长150米时，所用材料费最小。

2、求微分方程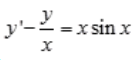满足初始条件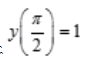的特解。

答 案：解：将方程改写为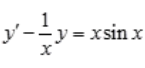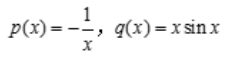，，则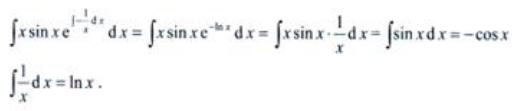故方程通解为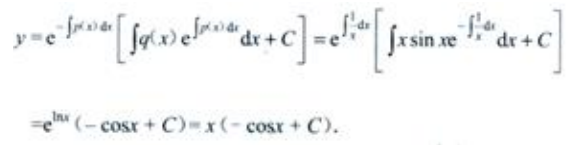将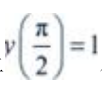代入通解，得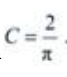从而所求满足初始条件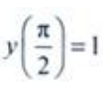的特解为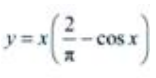

3、设f（x，y）为连续函数，交换二次积分的积分次序。

答 案：解：由题设知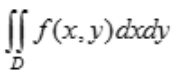中积分区域的图形应满足1≤x≤e，0≤y≤lnx，因此积分区域的图形见下图中阴影部分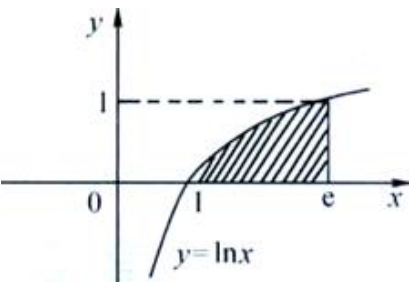．由y＝lnx，有x＝e^y。所以。

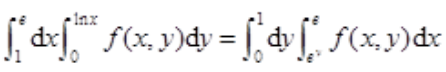填空题

1、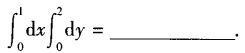  

答 案：2

解 析：本题考查的知识点为二次积分的计算。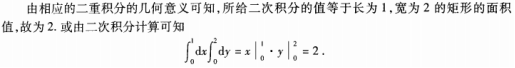  

2、微分方程dy＋xdx＝0的通解为（）。

答 案：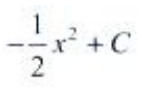

解 析：所给方程为可分离变量方程，分离变量得，dy＝-xdx，等式两边分别积分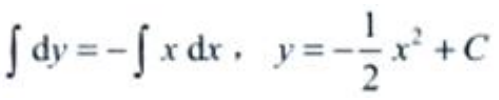

3、设y＝f（x）可导，点x₀=2为f（x）的极小值点，且f（2）＝3,则曲线y＝f（x）在点（2，3）处的切线方程为（）。

答 案：y＝3

解 析：由于y＝f（x）可导，且点x₀=2为f（x）的极小值点，由极值的必要条件可得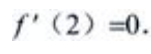又f（2）＝3，可知曲线过点（2，3）的切线方程为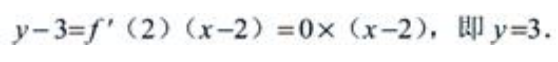

简答题

1、计算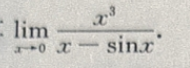  

答 案：