2023年成考高起点《数学(理)》每日一练试题02月18日

2023年成考高起点《数学(理)》每日一练试题02月18日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知点A(1,1),B(2,1)，C(—2,3)，则过点A及线段BC中点的直线方程为（）。

• A：x-y+2=0
• B：x+y-2=0
• C：x+y+2=0
• D：x-y=0

答 案：B

解 析：该小题主要考查的知识点为直线方程的两点式. 【考试指导】  

2、当圆锥的侧面积和底面积的比值是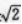时，圆锥轴截面的顶角是（ ）

• A：45°
• B：60°
• C：90°
• D：120°

答 案：C

解 析：求圆锥的轴截面的顶角，先画出轴截面(如下图)，可知轴截面为等腰三角形，圆锥嘲面是扇形，固锥底面的周长等于展开侧面的扇形的孤长．

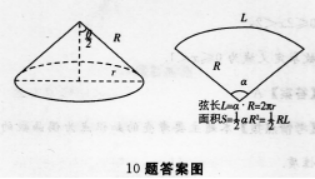
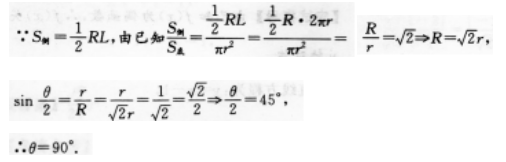
3、下列函数(　　)是非奇非偶函数。

• A：ƒ(x)=x
• B：ƒ(x)=x²-2｜x｜-1
• C：ƒ(x)=2^｜x｜
• D：ƒ(x)=2^x

答 案：D

解 析：

4、下列函数的图像向右平移一个单位长度之后，y=ƒ(x)的图像重合的是（）。

• A：y=ƒ(x+1)
• B：y=ƒ(x-1)
• C：y=ƒ(x)+1
• D：y=ƒ(x)-1

答 案：A

解 析：图像向右平移一个单位长度后与y=ƒ(x)的图像重合，即求y=ƒ(x)向左平移一个单位的函数表达式。由y=ƒ(x)图像向右平移|c|个单位，得y=ƒ(x+c)(c＜0)图像，向左平移c个单位，得y=ƒ(x+c)图像，向上平移c个单位，得y=ƒ(x)+c图像，向下平移|c|个单位，得y=ƒ(x)+c(c＜0)图像，反之：由y=ƒ(x+c)向右平移c个单位得y=ƒ(x)的图像。

主观题

1、已知a、b、c成等比数列，x是a、b的等差中项，y是b、c的等差中项，证明a/x+c/y=2。

答 案：由已知条件得，b2=ac，2x=a+b，2y=b+c①∴2cx=ac+bc，2ay=ab+ac。②②中两式相加得，2ay+2cx=ab+2ac+bc，又①中后两式相乘得，4xy=(a+b)(b+c)=ab+2ac+bc；
∴2ay+2cx=4xy，a/x+c/y=2。

2、等差数列{a_n}中，a₁=-393，a₂+a₃=-768，{b_n}是等比数列，q∈(0,1)，b1=2，{b_n}的前n项和为20，求：（Ⅰ）求a_n，b_n；
（Ⅱ）解不等式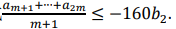

答 案：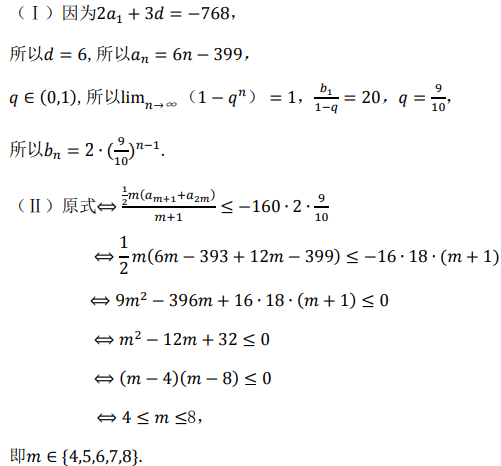

3、已知正六棱锥的高和底的边长都等于a，(Ⅰ)求它的对角面(过不相邻的两条侧棱的截面)的面积、全面积和体积；
(Ⅱ)求它的侧棱和底面所成的角，侧面和底面所成的角。

答 案：

4、

答 案：

填空题

1、函数f(x)=x²+bx+c的图像经过点(-1，0)，（3，0)，则f(x)的最小值为______。

答 案：-4

解 析：由于函数开口向上，故其在对称轴处取得最小值，又函数过点(-1，0)，(3，0)，故其对称轴为x=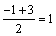，f_min(1)=1+b+C，而f(-1)由1-b+c=0，f(3)=9+3b+c=0，得b=-2，c=-3，故f_min（1)=1-2-3=-4.

2、从一批相同型号的钢管中抽取5根，测其内径，得到如下样本数据(单位：mm)： 110.8，109.4，111.2，109.5，109.1， 则该样本的方差为______mm2。

答 案：0.7

解 析：