2025年成考高起点《数学(文史)》每日一练试题12月02日
2025-12-02 12:17:45 来源:勒克斯教育网
2025年成考高起点《数学(文史)》每日一练试题12月02日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知sinx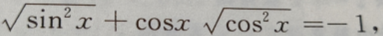 ,则x所在象限是()
,则x所在象限是()
- A:第一象限
- B:第二象限
- C:第三象限
- D:第四象限
答 案:C
解 析: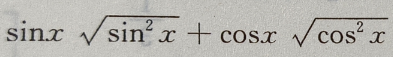 =sinx|sinx|+cosx|cosx|,当sinx、cosx均为负时,有
=sinx|sinx|+cosx|cosx|,当sinx、cosx均为负时,有 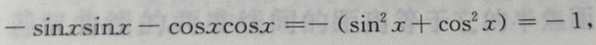 故x在第三象限
故x在第三象限
2、设甲:四边形ABCD是平行四边形,乙:四边形ABCD是正方形,则()。
- A:甲是乙的充分条件,但不是乙的必要条件
- B:甲是乙的必要条件,但不是乙的充分条件
- C:甲是乙的充分必要条件
- D:甲不是乙的充分条件,也不是乙的必要条件
答 案:B
3、一个袋子中装有标号分别为1,2,3,4的四个球,采用有放回的方式从袋中摸球两次,每次摸出一个球,则恰有一次摸出2号球的概率为()。
- A:
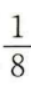
- B:

- C:
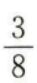
- D:

答 案:C
解 析:本题主要考查的知识点为独立重复试验的概率。 所求概率为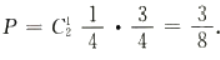
4、与圆x2+y2=4关于点M(3,2)成中心对称的曲线方程是( )
- A:
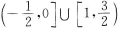
- B:
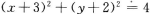
- C:
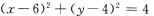
- D:
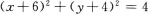
答 案:C
解 析:与圆关于点M成中心对称的曲线还是圆.只要求出圆心和半径,即可求出圆的方程.圆x2+y2=4的圆心(0,0)关于点M(3,2)成中心对称的点为(6,4),所以所求圆的圆心为(6,4),半径与对称圆的半径相等,所以所求圆的方程为(x-6)2+(y-4)2=4. 【考点指要】本题主要考查中心对称图形的定义、中点坐标公式的灵活运用、圆的标准方程的求法,这些主要概念在考试大纲中要求掌握,同时也是近几年经常考到的知识点.
主观题
1、设全集U=R,集合A={x|-5<x<5},B={x|0≤x≤7},求CUA∩B.
答 案:解:全集U=R,A={x|-5<x<5},B={X|0≤x≤7},因为CuA={x|x≤-5或x≥5},所以CuA∩B={x|x≤-5或x≥5}N{x|0≤x≤7}={x|5≤x≤7},如图1—10所示。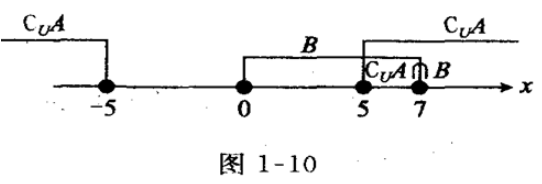
2、教室里有50人在开会,其中学生35人,家长12人,老师3人,现校长在门外听到有人在发言,那么发言人是老师或学生的概率为多少?
答 案:此题属于互斥事件,发言人是老师的概率为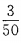 ,是学生的概率为
,是学生的概率为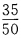 ,故所求概率为。
,故所求概率为。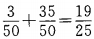
3、若tanα、tanβ是关于x的方程mx2-(2m-3)x+m-2=0的两个实根,求tan(α+β)的取值范围
答 案: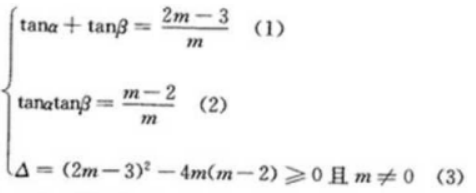 由(1)(2)得,tan(a+β)=m-3/2;由(3)得m≤9/4且m≠0所以tan(a+β)的取值范围是(-∞,-3/2)U(-3/2,3/4)
由(1)(2)得,tan(a+β)=m-3/2;由(3)得m≤9/4且m≠0所以tan(a+β)的取值范围是(-∞,-3/2)U(-3/2,3/4)
4、若双曲线 的两条准线将两个焦点的连线分成三等分,求双曲线的离心率。
的两条准线将两个焦点的连线分成三等分,求双曲线的离心率。
答 案:设双曲线的半焦距为c,则双曲线 【考点指要】本题要求根据双曲线的焦距、离心率、准线方程三者之间的关系进行计算,属较容易题,在成人高考中常见.
【考点指要】本题要求根据双曲线的焦距、离心率、准线方程三者之间的关系进行计算,属较容易题,在成人高考中常见.
填空题
1、在△ABC中,已知AB=3,BC=5,AC=7,则cosB=______。
答 案: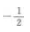
2、从甲、乙、丙3名学生中随机选2人,则甲被选中的概率为 .
答 案: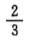
解 析: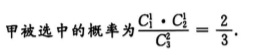
2025年成考高起点《数学(文史)》每日一练试题02月12日 02-12 2022年成考高起点《数学(文史)》每日一练试题12月02日 12-02 2023年成考高起点《数学(文史)》每日一练试题02月12日 02-12 2023年成考高起点《数学(文史)》每日一练试题12月02日 12-02 2024年成考高起点《数学(文史)》每日一练试题12月02日 12-02 2024年成考高起点《数学(文史)》每日一练试题02月12日 02-12 2025年成考高起点《数学(文史)》每日一练试题02月02日 02-02 2025年成考高起点《数学(文史)》每日一练试题02月01日 02-01



