2025年成考高起点《数学(理)》每日一练试题12月01日

2025年成考高起点《数学(理)》每日一练试题12月01日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、直线2x+y+m=0和直线x+2y+n=0的位置关系是（）。

• A：平行
• B：垂直
• C：相交但不垂直
• D：不确定

答 案：C

解 析：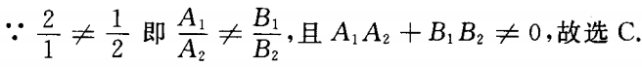

2、设f(x)=x³+ax²+x为奇函数，则a=（）。

• A：1
• B：0
• C：
• D：-2 D.C.-1

答 案：B

解 析：本题主要考查的知识点为函数的奇偶性. 因为f(x)为奇函数，故f(-x)=-f(x)。即-x³+ax²-x=-x³-ax²-x，a=0。

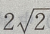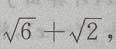
3、在△ABC中，若b=，c=则a等于（）

• A：2
• B：
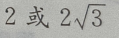
• C：
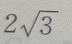
• D：无解

答 案：B

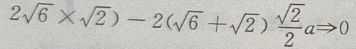
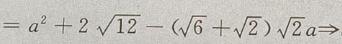
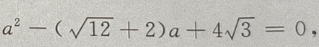解 析：此题是已知两边和其中一边的对角,解三角形时,会出现一解、两解、无解的情况,要注意这一点.用余弦定理可得解出

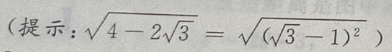
4、一部电影在4个单位轮映，每一单位放映一场，轮映次序有（）。

• A：4种
• B：16种
• C：24种
• D：256种

答 案：C

主观题

1、设a为实数，且tanα和tanβ是方程ax²+（2a-3）x+（a-2）=0的两个实根，求tan（α+β）的最小值。

答 案：由已知得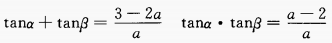

2、试证明下列各题
（1）
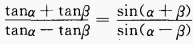
（2）

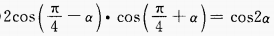
答 案：（1）化正切为正、余弦，通分即可得证。 （2）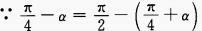

3、设分别讨论x→0及x→1时f（x）的极限是否存在？

答 案：∴f（x）在x=0处极限不存在 同理f（x）在x=1处极限存在

4、某气象预报站天气预报的准确率为80%，计算（1）5次预报中恰有4次准确的概率； （2）5次中至少有次准确的概率.(计算结果保留两个有效数字).  

答 案：  把每次预报看做一次试验，“预报结果准确”看成事件P（A）=0.8，本题就相当于在5次独立重复试验中求A恰好发生4次（或至少4次）的概率，此题属于独立重复试验，由公式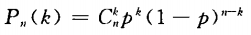来求解。 （1）n=5；p=0.8；k=4 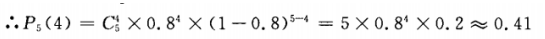即恰有4次准确的概率为0.41. (2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即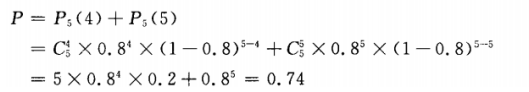 即至少有4次准确的概率为0.74。  

填空题

1、从甲、乙、丙3名学生中随机选2人，则甲被选中的概率为          .

答 案：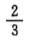

解 析：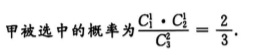

2、lg(tan43°tan45°tan47°)=（）  

答 案：0

解 析：lg(tan43°tan45°tan47°)=lg(tan43°tan45°cot43°)=lgtan45°=lg1=0