2025年成考高起点《数学(文史)》每日一练试题11月21日

2025年成考高起点《数学(文史)》每日一练试题11月21日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、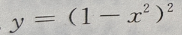的导数是  

• A：
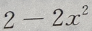
• B：
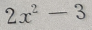
• C：
• D：

答 案：C

解 析：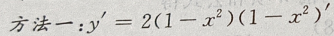

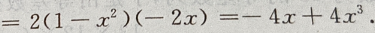
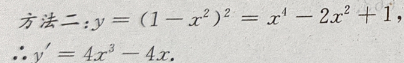
2、设集合 （）。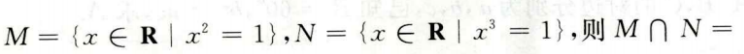

• A：{1}
• B：{-1}
• C：{—1，1）
• D：

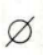
答 案：A

解 析：本题主要考查的知识点为集合的运算。 由题意M={-1，1}，N={1}，所以M∩N=（1}。  

3、设α=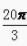，则（）。  

• A：sinα＞0，cosα＜0
• B：sinα＞0，cosα＞0
• C：sinα＜0，cosα＞0
• D：sinα＜0，cosα＜0

答 案：A

4、函数y=cos⁴x-sin⁴x（x∈R）的最小正周期为（）。

• A：
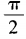
• B：π
• C：2π
• D：4π

答 案：B

解 析：y=（cos²x+sin²x）（cos²x-sin²x）=cos2x， 所以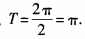

主观题

1、若双曲线的两条准线将两个焦点的连线分成三等分,求双曲线的离心率。

答 案：设双曲线的半焦距为c，则双曲线 【考点指要】本题要求根据双曲线的焦距、离心率、准线方程三者之间的关系进行计算，属较容易题，在成人高考中常见．

2、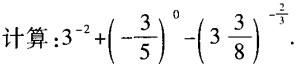  

答 案：

3、若tanα、tanβ是关于x的方程mx²-(2m-3)x+m-2=0的两个实根，求tan(α+β)的取值范围

答 案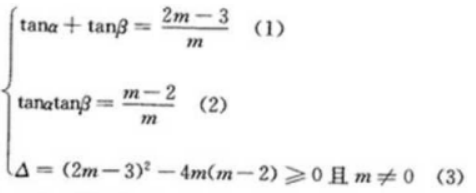： 由(1)(2)得，tan(a+β)=m-3/2;由(3)得m≤9/4且m≠0所以tan(a+β)的取值范围是(-∞，-3/2)U(-3/2，3/4)  

4、已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。  

答 案：由已知，得

填空题

1、直线的倾斜角的度数为（）  

答 案：60°

解 析：由题意知直线的斜率为设直线的倾斜角为α，则tanα=由0°≤α≤180°，故α=60°

2、与已知直线7x+24y-5=0平行，且距离等于3的直线方程是______。  

答 案：7x+24y+70=0或7x+24y-80=0

解 析：设要求的直线方程为7x+24y+c=0， ∵直线7x+24y+c=0到直线7x+24y-5=0的距离等于3 ∴ ∴.C=70或-80. 故所求的直线方程为7x+24y+70=0或7x+24y-80=0