2025年成考高起点《数学(文史)》每日一练试题11月13日
2025-11-13 12:06:45 来源:勒克斯教育网
2025年成考高起点《数学(文史)》每日一练试题11月13日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、函数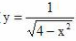 的定义域为()。
的定义域为()。
- A:(-∞,-4)∪(4,+∞)
- B:(-∞,-2)∪(2,+∞)
- C:[-2,2]
- D:(-2,2)
答 案:D
2、不等式|x-1|<7的解集为
- A:{x|-10
- B:{x|-8
- C:{x|-6
- D:{x|6
- B:{x|-8
答 案:C
解 析:|x-1|<7 ⇒ -7
3、已知sinα= 且
且 ,则tanα的值等于()。
,则tanα的值等于()。
- A:

- B:

- C:

- D:

答 案:D
4、下面四个关系式其中正确的个数为()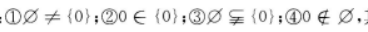
- A:4
- B:3
- C:2
- D:1
答 案:A
解 析:
主观题
1、求函数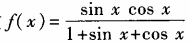 (x∈R)的最大值与最小值。
(x∈R)的最大值与最小值。
答 案:设sinx+cosx=t,则(sinx+cosx)2=t2,1+2sinxcosx=t2,sinxcosx= 于是转化为求
于是转化为求 的最值。
由所设知
的最值。
由所设知 上为增函数,故g(t)的最大值为
上为增函数,故g(t)的最大值为 最小值为
最小值为
2、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.
的焦点,且与C交于A,B两点.
(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 得
得 设A(x1,y1).B(x2,y2),则
设A(x1,y1).B(x2,y2),则 因此
因此
3、等差数列{an}的通项公式为an=3n-1,在{an}中,每相邻的两项之间插人三项,构成新的等差数列{bn}. (Ⅰ)求{bn}的通项公式; (Ⅱ)求{bn}前10项的和.
答 案: 考点本题主要考查等差数列的通项公式和前n项和公式的运用,是成人高考常见题型.
考点本题主要考查等差数列的通项公式和前n项和公式的运用,是成人高考常见题型.
4、设全集U=R,集合A={x|-5<x<5},B={x|0≤x≤7},求CUA∩B.
答 案:解:全集U=R,A={x|-5<x<5},B={X|0≤x≤7},因为CuA={x|x≤-5或x≥5},所以CuA∩B={x|x≤-5或x≥5}N{x|0≤x≤7}={x|5≤x≤7},如图1—10所示。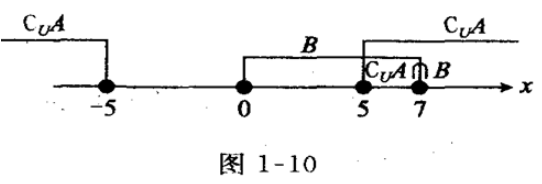
填空题
1、某人投篮每次命中率为0.8,现独立投篮4次,恰好命中3次的概率是______。
答 案:0.4096
解 析:本题试验属于独立重复试验,其概率为 
2、101-lg2=______。
答 案:5
解 析: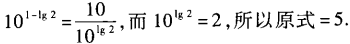
2022年成考高起点《数学(文史)》每日一练试题11月13日 11-13 2024年成考高起点《数学(文史)》每日一练试题11月13日 11-13 2023年成考高起点《数学(文史)》每日一练试题11月13日 11-13 2025年成考高起点《数学(文史)》每日一练试题09月13日 09-13 2025年成考高起点《数学(文史)》每日一练试题01月13日 01-13 2025年成考高起点《数学(文史)》每日一练试题04月13日 04-13 2025年成考高起点《数学(文史)》每日一练试题03月13日 03-13 2025年成考高起点《数学(文史)》每日一练试题05月13日 05-13



