2025年成考高起点《数学(理)》每日一练试题10月01日

2025年成考高起点《数学(理)》每日一练试题10月01日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

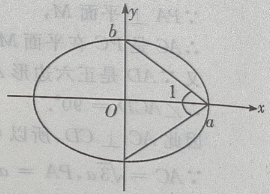
1、从椭圆与x轴额右交点看短轴两端点的视角为60°的椭圆的离心率（）  

• A：
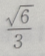
• B：
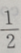
• C：1
• D：

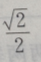
答 案：A

解 析：求椭圆的离心率,先求出a,c.(如图) 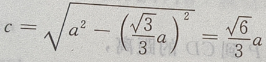，由椭圆定义知

2、曲线y=x+2在点（1，2）处的切线斜率为（）。

• A：1
• B：2
• C：-1
• D：4

答 案：A

解 析：方法一：∵y=x+2，k=y’＝1 方法二：也可用直线方程y=kx+b直接得出k=1。  

3、下列函数中，为增函数的是（）。

• A：y=x³
• B：y=x²
• C：y=-x²
• D：y=-x³

答 案：A

解 析：本题主要考查的知识点为函数的单调性. 对于y=x³，y’=3x²≥0，故y=x³为增函数

4、设集合M＝{0，1，2，3，4}，N＝{1，2，3}，T＝{2，4，6}，则集合（M∩T）∪N＝（）。  

• A：{0，1，2，3，4，6}
• B：{1，2，3，4}
• C：{2，4}
• D：{2，4，6}

答 案：B

解 析：M∩T＝（2，4），则集合（M∩T）∪N＝{1，2，3，4}。答案为B。  

主观题

1、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由，得设A（x1,y1），B（x2,y2），则因此

2、

答 案：

解 析：

3、求函数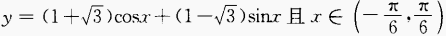上的最大值以及取得这个最大值的x。

答 案：.1 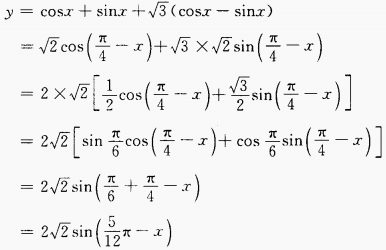函数取最大值，即y最大值=。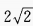

4、当自变量为何值时，函数y=2x³-3x²-12x+21有极值，其极值为多少？  

答 案：y'=6x²-6x-12=6（x-2）（x+1） 当x<-1或x>2时，y>0，当-1 故当x=-1时有极大值，其值为f（-1）=28 当x=2时有极小值，其值为f（2）=1

填空题

1、若tanα-cotα=1，则=______。

答 案：4

解 析：由立方差公式得,tan³α-cot³α=(tana-cotα)(tan²α+tanαcota+cot²α)(tana-cotα)[(tanα-cotα)²+3tanαcotα]=4  

2、已知函数y=a²+bx+c的图像是以(6,-12)为顶点的抛物线，并且与x轴的一个交点坐标是(8,0)，则a=()，b=()，c=()

答 案：  3；-36；96  

解 析：根据顶点坐标是（6，-12），设y=a(x-6)²-12(8,0)代入得：0=a*(8-6)²-12得到a=3
即y=3(x-6)²-12=3x²-36x+96
故a=3,b=-36,c=96