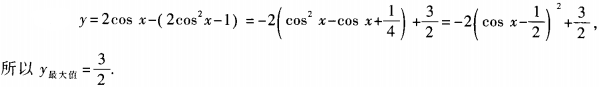2025年成考高起点《数学(理)》每日一练试题08月17日

2025年成考高起点《数学(理)》每日一练试题08月17日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若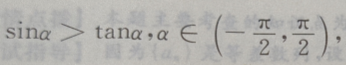则（）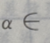

• A：
• B：
• C：
• D：

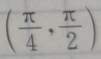
答 案：B

解 析：首先做出单位圆,然后根据问题的约束条件,利用三角函数线找出满足条件的a角取值范围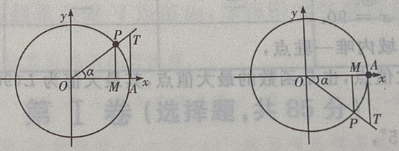  

2、设双曲线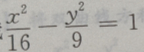的渐近线的斜率为k，则|k|=（）  

• A：
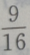
• B：
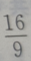
• C：
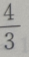
• D：

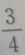
答 案：D

解 析：双曲线渐近线的斜率为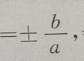k故本题中k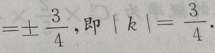

3、下列各式的值为零的是（）。

• A：0⁰
• B：log₁1
• C：
• D：log₂|-1|

答 案：D

解 析：0⁰和log₁1均没有意义，可排除（A）、（B），而（2-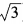）⁰=1。故选D。

4、函数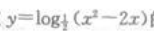的定义域是（）。

• A：(－∞，0）∪[2，＋∞)
• B：[0，2]
• C：(－∞，0)∪（2，＋∞)
• D：(0，2)

答 案：C

解 析：x²－2x＞0，解得x＜0或x＞2．函数的定义域为(－∞，0)∪(2，＋∞)。答案为C。

主观题

1、设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．

答 案：(I）f(1)=1,f'(x)=2+lnx，故f'(1)=2.所以曲线y=f(x）在点（1,f(1))处的切线方程为y=2x-1.(II）令f'(x)=0，解得当时，f'(x)时，f'(x)＞O.故f(x）在区间单调递减，在区间单调递增．因此f(x）在时取得极小值

2、化简： （1）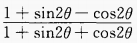
（2）

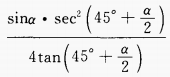
答 案：（1） （2）

3、已知a,b,c成等差数列，a,b,c+1成等比数列．若b=6，求a和c．

答 案：由已知得解得

4、已知数列的前n项和 求证：是等差数列，并求公差和首项。  

答 案：  

填空题

1、一个问题在1小时内，甲能独立解决的概率是0.5，乙能独立解决的概率是0.4，两人在1小时内解决问题的概率是______。  

答 案：0.7

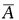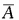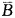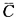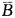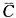解 析：设事件A为两人在1小时内解决问题，即1小时内至少有一人能解决问题，事件B为甲在1小时内解决问题，事件C为乙在1小时内解决问题，事件B、C是相互独立事件，事件A的对立事件 互为在1小时内两个人都没有解决问题，所以 P（A）=1-P（）=1-P（·）=1-P（）·P（） =1-（1-0.5）×（1-0.4）=1-（0.5×0.6）=1-0.3=0.7

2、函数y=2cosx-cos2x（x∈R）的最大值为______。  

答 案：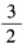

解 析：