2025年成考高起点《数学(理)》每日一练试题07月03日

2025年成考高起点《数学(理)》每日一练试题07月03日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知a，b为任意正实数，则下列等式中恒成立的是（）。

• A：a^b=b^a
• B：2^a+b=2^a+2^b
• C：
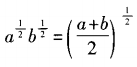
• D：a^lgb=b^lga

答 案：D

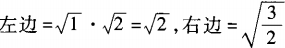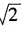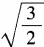解 析：由于a，b为任意正实数，不妨取a=1，b=2。在A项中，1²≠2¹；B项中，2¹⁺²≠2¹+2²；C项中，，而≠。故选D。

2、两条直线是异面直线的充分条件是这两条直线（）。

• A：分别在两个平面内
• B：是分别在两个相交平面内的不相交的直线
• C：是分别在两个相交平面内的不平行的直线
• D：分别在两个相交平面内，其中一条与这两个平面的交线相交于一点，而另一条不过这个点

答 案：D

3、函数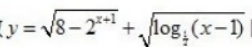的定义域为（）。

• A：{x|x>1}
• B：{x|x≤2}
• C：{x|1
• D：{x|1

答 案：D

4、在△ABC中，若lgsinA-lgsinB-lgcos=lg2，则△ABC是（）

• A：以A为直角的三角形
• B：b=c的等腰三角形
• C：等边三角形
• D：钝角三角形

答 案：B

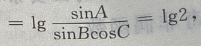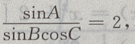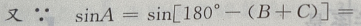
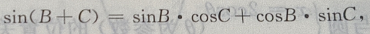
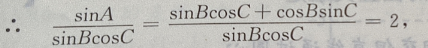
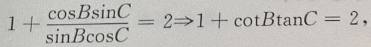
解 析：判断三角形的形状，条件是用一个对数等式给出先将对数式利用对数的运算法则整理。 ∵lgsinA-lgsinB-lgcos=lg2，由对数运算法则可得,左 两个对数底数相等则真数相等：即2sinBcosC=sinA 在△ABC中，∵A+B+C=180°，∴A=180°-（B+C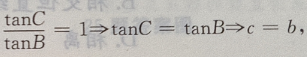）, 故为等腰三角形

主观题

1、已知log₅3=a，log₅4=b，求log₂₅12关于a，b的表达式。  

答 案：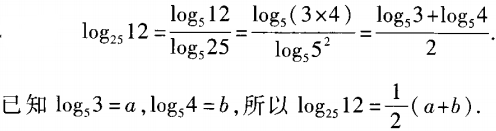

2、

答 案：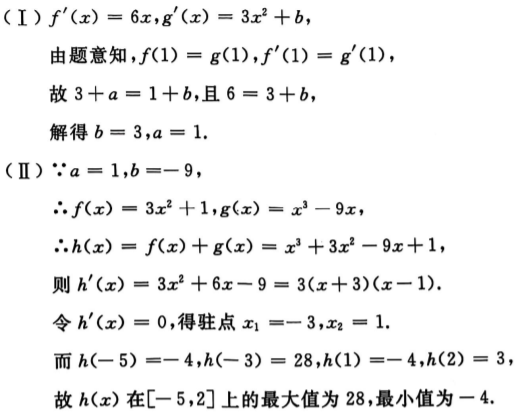

解 析：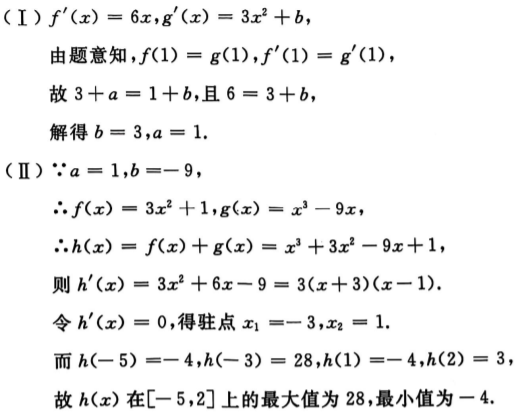

3、计算 （1）tan5°+ cot5°- 2sec80°
（2）tan15°+cot15
（3）sin15°sin75°

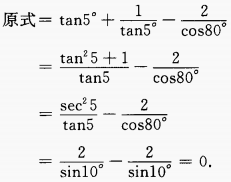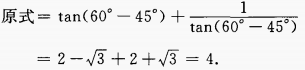答 案：（1）化切割为弦进行运算。 （2） （3）

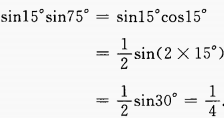
4、已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。

答 案：由已知，得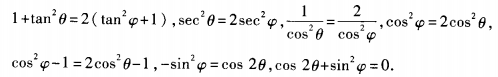

填空题

1、若tanα-cotα=1，则=______。

答 案：4

解 析：由立方差公式得,tan³α-cot³α=(tana-cotα)(tan²α+tanαcota+cot²α)(tana-cotα)[(tanα-cotα)²+3tanαcotα]=4  

2、y=ax²-bx+c的导数y'|x=1=______。

答 案：2a-b