2025年成考高起点《数学(理)》每日一练试题06月28日

2025年成考高起点《数学(理)》每日一练试题06月28日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、方程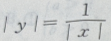的图像是下图中的（）  

• A：
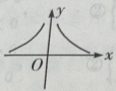
• B：
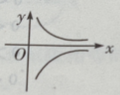
• C：
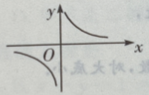
• D：

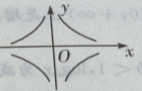
答 案：D

解 析：本题属于读图题型，在寻求答案时,要着重讨论方程的表达式  

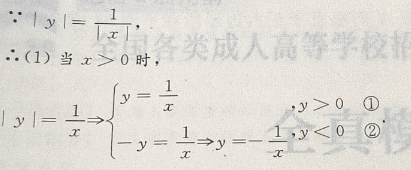
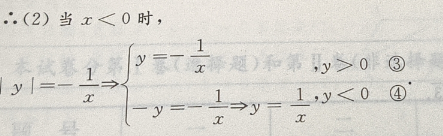
2、已知全集U=R，A={x|x≥1}，B={x|-1

• A：{x|x≤2}
• B：{x|x<2}
• C：{x|-1
• D：{x|-1

答 案：A

解 析：补集运算应明确知道是否包括端点.A在U中的补集是x<1，  

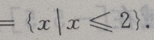
3、抛物线y²=2px上任意一点与焦点连线中点的轨迹方程是（）。

• A：
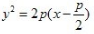
• B：
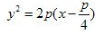
• C：
• D：

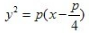
答 案：D

4、若f(x)为偶函数，且在(0，＋∞)为增函数，则下列不等式成立的是（）。

• A：
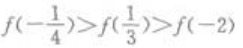
• B：
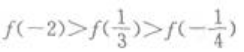
• C：
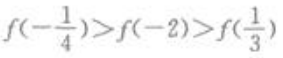
• D：

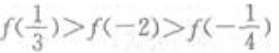
答 案：B

解 析：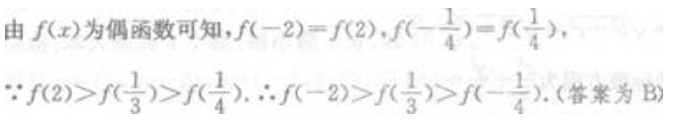

主观题

1、设分别讨论x→0及x→1时f（x）的极限是否存在？

答 案：∴f（x）在x=0处极限不存在 同理f（x）在x=1处极限存在

2、在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量关于基底{a,b,c}的分解式 （Ⅱ）求证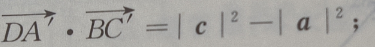： （Ⅲ）求证：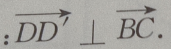  

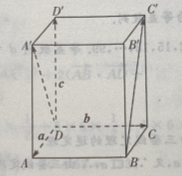
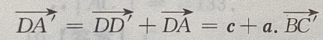
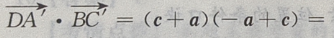
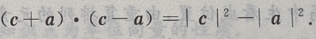答 案：(Ⅰ)由题意知(如图所示) (Ⅱ) (Ⅲ)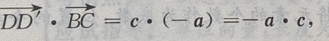 由已知，a,c是正四棱柱的棱，a,b,c两两垂直  

3、记△ABC的内角A，B，C的对边分别为a，b，c，已知B=60°，b²=ac，求A。    

答 案：由余弦定理b²=a²+c²-2accosB，可得ac=a²+c²-ac，即a²+c²-2ac=(a-c)²=0，解得a=c。 又因为B=60°，故△ABC为等边三角形，所以A=60°

4、求（1+tan10°）（1+tan35°）的值。  

答 案：原式=1+tan10°+tan35°+tan10°·tan35°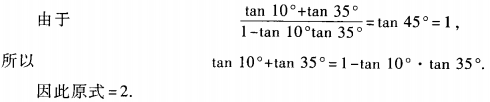

填空题

1、lgsinθ=a,lgcosθ=b，则sin2θ=______。  

答 案：2×10^a+b

解 析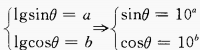： sin2θ=2sinθcosθ=2×10^a×10^b=2×10^a+b  

2、一个问题在1小时内，甲能独立解决的概率是0.5，乙能独立解决的概率是0.4，两人在1小时内解决问题的概率是______。  

答 案：0.7

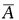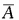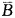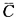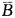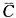解 析：设事件A为两人在1小时内解决问题，即1小时内至少有一人能解决问题，事件B为甲在1小时内解决问题，事件C为乙在1小时内解决问题，事件B、C是相互独立事件，事件A的对立事件 互为在1小时内两个人都没有解决问题，所以 P（A）=1-P（）=1-P（·）=1-P（）·P（） =1-（1-0.5）×（1-0.4）=1-（0.5×0.6）=1-0.3=0.7