2025年成考高起点《数学(理)》每日一练试题06月26日

2025年成考高起点《数学(理)》每日一练试题06月26日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、下列各式中正确是（）。

• A：
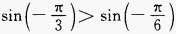
• B：
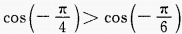
• C：
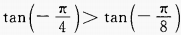
• D：

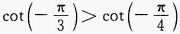
答 案：D

解 析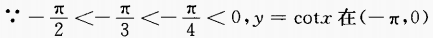： 上为减函数，故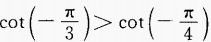

2、（）。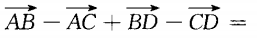

• A：0
• B：
• C：
• D：

答 案：A

解 析：

3、抛物线y²=2px上任意一点与焦点连线中点的轨迹方程是（）。

• A：
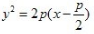
• B：
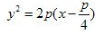
• C：
• D：

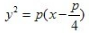
答 案：D

4、二项式(2x－1)⁶的展开式中，含x⁴项系数是（）。

• A：-15
• B：-240
• C：15
• D：240

答 案：D

解 析：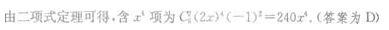

主观题

1、当自变量为何值时，函数y=2x³-3x²-12x+21有极值，其极值为多少？  

答 案：y'=6x²-6x-12=6（x-2）（x+1） 当x<-1或x>2时，y>0，当-1 故当x=-1时有极大值，其值为f（-1）=28 当x=2时有极小值，其值为f（2）=1

2、求下列函数的最大值、最小值和最小正周期： （1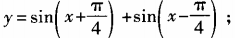）（2）y=6cosx+8sinx

答 案：  

3、求（1+tan10°）（1+tan35°）的值。  

答 案：原式=1+tan10°+tan35°+tan10°·tan35°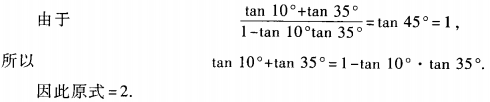

4、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得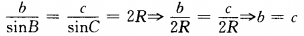

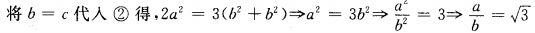
∴a：b=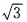：1
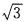于是a：b：c=：1：1。  

填空题

1、100件产品中有3件次品，每次抽取一件，有放回的抽取三次，恰有1件是次品的概率是______。  

答 案：0.0847

解 析：由于三次抽取是独立的，每次抽取可看做是一次试验，每次试验只有两个可能结果：“正品”或“次品”，次品率为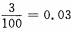，因此二次独立且重复试验恰有1件次品率为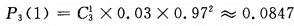  

2、

答 案：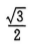

解 析：