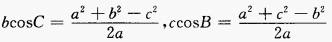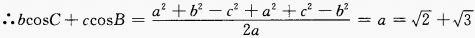2025年成考高起点《数学(理)》每日一练试题04月01日
2025-04-01 12:10:44 来源:勒克斯教育网
2025年成考高起点《数学(理)》每日一练试题04月01日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、在△ABC中,若lgsinA-lgsinB-lgcos=lg2,则△ABC是()
- A:以A为直角的三角形
- B:b=c的等腰三角形
- C:等边三角形
- D:钝角三角形
答 案:B
解 析:判断三角形的形状,条件是用一个对数等式给出先将对数式利用对数的运算法则整理。 ∵lgsinA-lgsinB-lgcos=lg2,由对数运算法则可得,左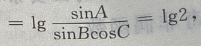 两个对数底数相等则真数相等:
两个对数底数相等则真数相等: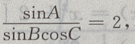 即2sinBcosC=sinA
在△ABC中,∵A+B+C=180°,∴A=180°-(B+C),
即2sinBcosC=sinA
在△ABC中,∵A+B+C=180°,∴A=180°-(B+C),
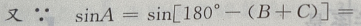
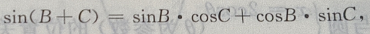
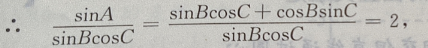
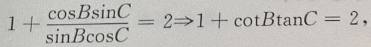
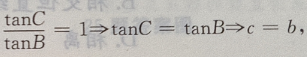 故为等腰三角形
故为等腰三角形
2、设α是第三象限角,若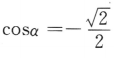 ,则sinα=()
,则sinα=()
- A:
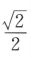
- B:

- C:
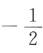
- D:
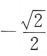
答 案:D
解 析:由于 ,而α为第三象限角,故
,而α为第三象限角,故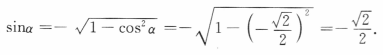
3、在△ABC中,已知2B= A+C, = ac,则B-A=()
= ac,则B-A=()
- A:0
- B:
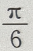
- C:
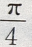
- D:
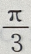
答 案:A
解 析:在△ABC中,A+B+C=π,A+C=π-B,① 因为2B=A+C,②
由①②得2B=π-B,
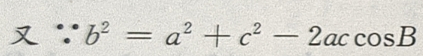
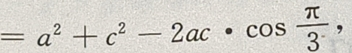
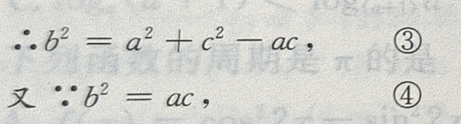 由③④得
由③④得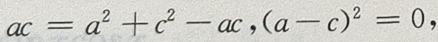 a=c。所以A=C,又
a=c。所以A=C,又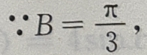 所以△ABC为等边三角形,则B-A=0
所以△ABC为等边三角形,则B-A=0
4、已知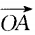 =(3,2),
=(3,2),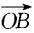 =(-4,y),并其人
=(-4,y),并其人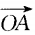 ⊥
⊥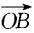 ,则
,则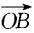 的长度为()。
的长度为()。
- A:
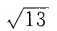
- B:
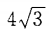
- C:
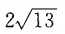
- D:
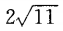
答 案:C
解 析: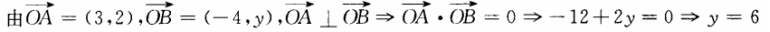
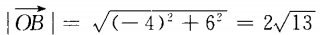
主观题
1、求下列函数的最大值、最小值和最小正周期: (1)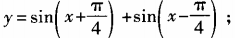 (2)y=6cosx+8sinx
(2)y=6cosx+8sinx
答 案:
2、已知a,b,c成等差数列,a,b,c+1成等比数列.若b=6,求a和c.
答 案:由已知得 解得
解得
3、在正四棱柱ABCD-A'B'C'D'中, (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证:
答 案:(Ⅰ)由题意知(如图所示) 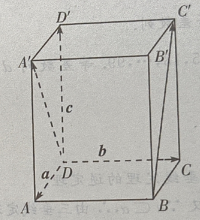
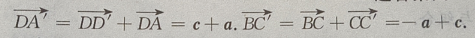
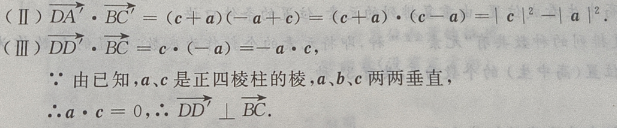
4、已知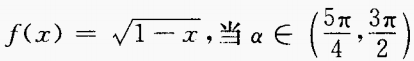 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。
答 案:由已知得, 填空题 1、在△ABC中,已知a= 答 案: 解 析:由余弦定理得, 2、cos267.5°- 0.5=______。 答 案: 解 析: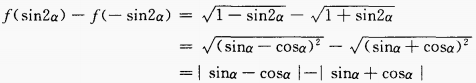
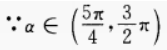 ∴sinα
∴sinα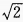 +
+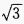 ,则bcosC+ccosB=______。
,则bcosC+ccosB=______。