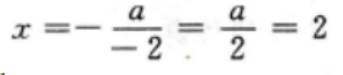2024年成考高起点《数学(理)》每日一练试题12月24日
2024-12-24 12:22:59 来源：勒克斯教育网
2024年成考高起点《数学(理)》每日一练试题12月24日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、在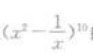
的展开式中,含x5项的系数是（）。
- A：1
- B：-1
- C：252
- D：-252
答 案：D
解 析：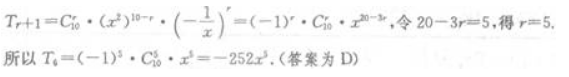
2、二项式(2x－1)6的展开式中，含x4项系数是（）。
- A：-15
- B：-240
- C：15
- D：240
答 案：D
解 析：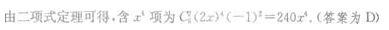
3、已知3sin2α+8sinα-3=0，则cos2α=（）。
- A：
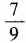
- B：
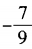
- C：
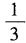
- D：
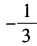
答 案：A
解 析：由已知得（3sinα-1）（sinα+3）=0。 由于|sinα|≤1，所以sinα=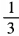
。因此
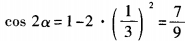。故选A。
4、下列各式的值为零的是（）。
- A：00
- B：log11
- C：
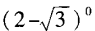
- D：log2|-1|
答 案：D
解 析：00和log11均没有意义，可排除（A）、（B），而（2-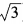
）0=1。故选D。
主观题
1、已知空间四边形OABC，OB=OC且∠AOB=∠AOC=θ（如图）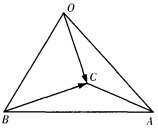
。求证：OA⊥BC。
答 案：
2、求下列函数的定义域： （1）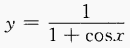
（2）
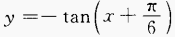
（3）
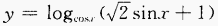
答 案：（1）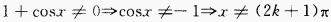 
∴函数的定义域为
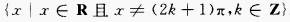（2） 
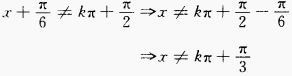∴函数的定义域为
（3）
由对数函数的性质知，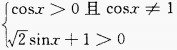
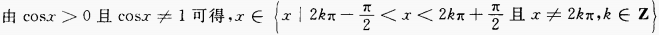
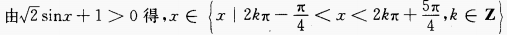故函数的定义域为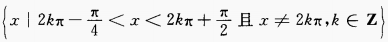
3、已知tan2θ=2tan2ψ+1，求cos2θ+sin2ψ的值。
答 案：由已知，得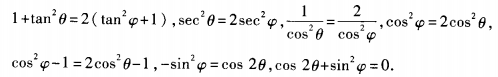 
4、函数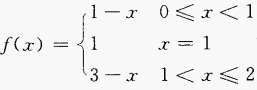
在其定义域上是否连续？作出f（x）的图形。
答 案：f（x）的定义域为[0，2] 当0≤x<1时f（x）=1-x是连续的 当1
填空题
1、lgsinθ=a,lgcosθ=b，则sin2θ=______。
答 案：2×10a+b
解 析：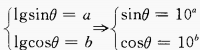
sin2θ=2sinθcosθ=2×10a×10b=2×10a+b
2、函数y=-x2+ax图像的对称轴为x=2，则a=______。
答 案：4
解 析：本题主要考查的知识点为二次函数的性质
由题意，该函数图像的对称轴为
- 备考交流
-
2025成考内部交流群群号：665429327
扫一扫或点击二维码入群
