2022年成考高起点《数学(理)》每日一练试题09月02日

2022年成考高起点《数学(理)》每日一练试题09月02日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、设0＜x＜l，则（）

• A：log_2x＞0
• B：0＜2^x＜1
• C：
• D：1＜2^x＜2

答 案：D

解 析：当0＜x＜1时，1＜2^x＜2，log₂x＜0，.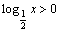

2、

• A：
• B：
• C：
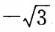
• D：

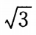
答 案：A

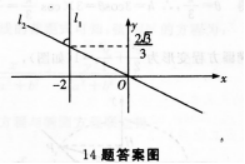
3、已知直线l₁与l₂的夹角是( )

• A：45°
• B：60°
• C：120°
• D：150°

答 案：B

解 析：直线l₁与l₂相交所成的锐角或直角叫做l₁与l₂的夹角，即0°≤θ≤90°，而选项C、D都大于90°,∴C、D排除， ∵l1的斜率不存在，所以不能用tanθ=

4、直三棱柱的每个侧面的面积为5，底面积是10，全面积是（）。

• A：15
• B：20
• C：25
• D：35

答 案：D

解 析：求全面积=侧面积+2底面积=5×3+10×2=35，应选D。误选C，错误的原因是只加了一个底面的面积。

主观题

1、已知数列{an}的前n项和 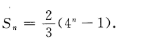(1)求{an}的通项公式; (2)若ak=128，求k。

答 案：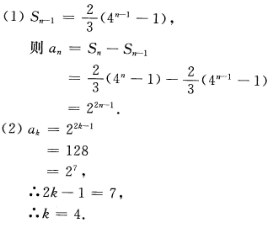

2、设函数(Ⅰ)求m;(Ⅱ)求f(x)的单调区间.

答 案：

3、

答 案：

4、电流强度I随时间t变化的函数关系式是I=Asinωt，设ω=100π(弧度／秒)，A=5(安培)。(Ⅰ)求电流强度I变化周期与频率；
(Ⅱ)当t=0,1/200,1/100,3/200,1/50(秒)时，求电流强度I(安培)；
(Ⅲ)画出电流强度I随时间t变化的函数的图像。

答 案：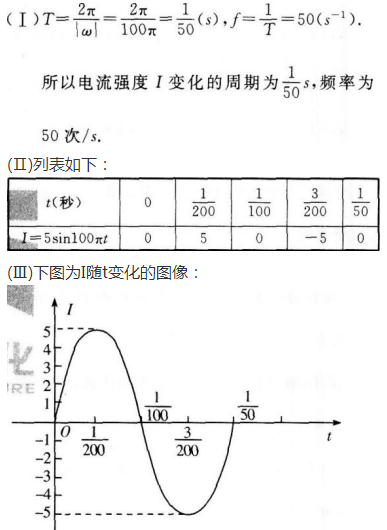

填空题

1、从某大学篮球队历次比赛得分中，抽取了8场比赛的得分作为样本，数据如下：88，74，73，87，70，72，86，90，则该样本的方差为（）。

答 案：62.25

解 析：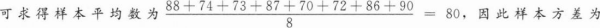

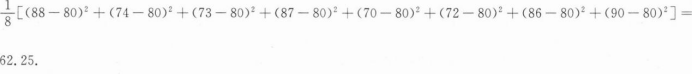
2、从一个正方体中截去四个三棱锥，得一正三棱锥ABCD，正三棱锥的体积是正方体体积的(  )。

答 案：1/3

解 析：截去的四个三棱锥的体积相等，其中任一个三棱锥都是底面为直角三角形,且直角边长与这个三棱锥的高相等，都等于正方体的棱长．设正方体的棱长为a，则截去的一个三棱锥的体积为